* 이진트리에서 루트노드인지 이너노드인지 잎새노드인지 구분하는 문제

루트노드 : 부모노드가 없는 경우, P가 NULL인 경우

이너노드 : 부모노드에 있는 수, P컬럼에 있는 수

잎새노드 : 그 외

SELECT N,
CASE WHEN P IS NULL THEN 'Root' 
    WHEN N IN (SELECT DISTINCT P FROM BST) THEN 'Inner'
    ELSE 'Leaf'
END
FROM BST
ORDER BY N

* 전체 CITY의 수(중복) 에서 고유 CITY 수를 빼는 문제 

SELECT COUNT(CITY) - COUNT(DISTINCT(CITY))
FROM STATION;

문제 

n크기의 배열에서, a ~ b까지의 인덱스에 k 만큼 더한 후 가장 큰 값을 리턴하는 문제

ex)

입력 : int n = 10, int [] queries

합계가 가장 큰 값은 인덱스 4,5에 해당하는 10이 됨

arr[1] = 3

arr[2] = 3

arr[3] = 3

arr[4] = 3 + 7=10

arr[5] = 3 + 7=10

arr[6] = 7 + 1 = 8

arr[7] = 7 + 1 = 8

arr[8] = 7 + 1 = 8

arr[9] = 1

arr[10] = 0

풀이방법

a인덱스에 k값을 넣고 b+1 인덱스에 -k값을 넣음

n크기인 배열의 누적합 중 가장 큰 값을 리턴

최댓값만 구하는 것이기 때문에 값이 언제 들어가는지만 유의하면 된다.

예를들어 1 ~ 4인덱스까지만 3을 추가한다면 1 ~ 5 인덱스의 각 합은 3, 3, 3, 3, 0이다.

누적합으로 구하게 되면 인덱스 1에서 +3 , 인덱스 2 ~ 4 는 +0으로 누적합 유지,

인덱스 5에서는 -3을 하여 누적합을 0으로 만들 수 있다.

인덱스 누적합

arr[1] = 3

arr[2] = 3 + 0

arr[3] = 3 + 0

arr[4] = 3 + 7=10

arr[5] = 10 + 0

arr[6] = 10 - 3 + 1 = 8

arr[7] = 8 + 0

arr[8] = 8 + 0

arr[9] = 8 - 7

arr[10] = 1 - 1

답

문제 : magazine 배열에 note 배열값들이 다 들어있는지 여부

해결법 :

1. magazine 배열의 값을 dictionary에 넣는다. key값으로,

magazine 배열의 중복된 문자값의 개수는 value로

2. note 배열의 값과 dictionary의 값을 비교한다. key값에 note배열의 값이 없거나,

dicitonary value값보다 더 많이 들어있을 때 No 출력

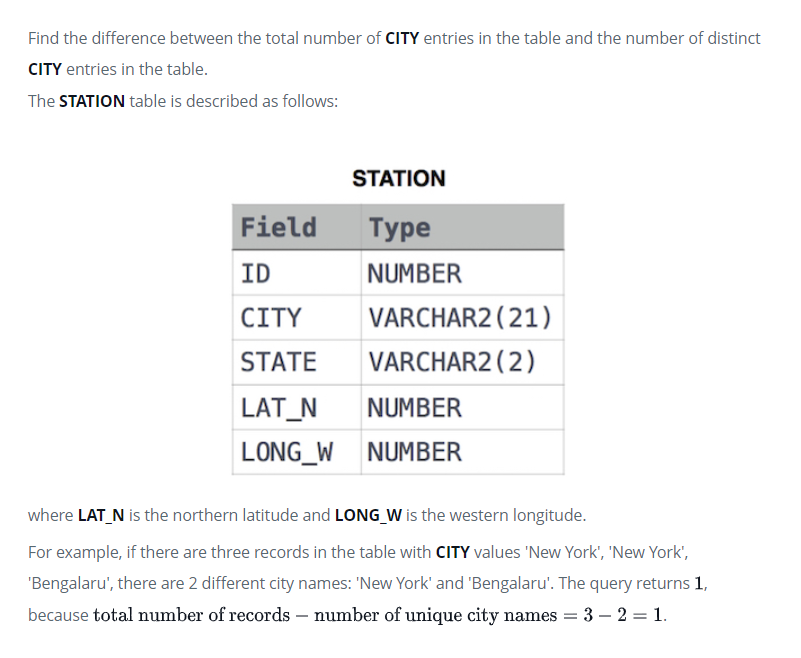
문제 요약

1, 2, 3, 4, 5...의 데이터가 담겨있는 int형 배열 q[]

뒤의 숫자는 앞으로 최대 두 칸까지 이동할 수 있다.

세 칸 이상 이동 시 : Too chaotic 출력

그 외 : 앞으로 이동한 횟수를 출력

Too chaotic 출력

각 숫자 i는 i - 1 인덱스에 위치한다.

   숫자 4는, 현재 3인덱스에 위치 ( q[3] = 4)

   숫자 4는 최대 두 칸 앞으로 이동할 수 있으므로

   인덱스 2, 1에 위치할 수 있다. ( q[2] = 4, q[1] = 4 가능)

   인덱스 0에 위치 시 Too chaotic( q[0] = 4인 경우 Too chaotic)

즉 q[i] - 1 - i > 2 일 때 Too chaotic이 출력되도록 한다.

birbe출력

q[j] > q[i] (j < i) 인 이유

처음 배열 q의 값들은 오름차순으로 정렬되어있어 앞의 값이 뒤의 값보다 작다.

하지만 배열 q의 값들이 앞으로 이동했을 경우 앞의 값이 뒤의 값보다 큰 경우가 발생

따라서 q[0] ~ q[i - 1] 중에서 q[i]의 값보다 큰 값의 개수를 세어 보면 이동한 숫자를 알 수 있다.

ex) 현재 q[] = {1, 2, 3, 4, 5}

숫자 4가 앞으로 한 칸 이동 

q[] = {1, 2, 4, 3, 5}

= 숫자 1 앞에 1보다 큰 값 없음

  숫자 2 앞에 2보다 큰 값 없음

  숫자 4 앞에 4보다 큰 값 없음

  숫자 3 앞에 3보다 큰 값은 4 하나

  숫자 5 앞에 5보다 큰 값 없음

= 총 한 번 이동

숫자 4가 앞으로 두 칸 이동

q[] = {1, 4, 2, 3, 5}

= 숫자 1 앞에 1보다 큰 값 없음

  숫자 4 앞에 4보다 큰 값 없음

  숫자 2 앞에 2보다 큰 값 4 하나

  숫자 3 앞에 3보다 큰 값은 4 하나

  숫자 5 앞에 5보다 큰 값 없음

= 총 두 번 이동

Max(0, q[i] - 2)의 이유

앞의 값과 비교할 때 q[0] ~ q[i - 1]까지 계속 비교할 필요가 없음

최대 앞으로 두칸 이동할 수 있기 때문에

q[i] - 2 부터 비교하면 됨

ex)

q[i]가 4일 때 4보다 큰 값은 5, 6, 7...이 있음

5는 최대 q[2]까지만, 6은 q[3]까지만 이동 가능

즉, q[2]이부터 q[i - 1]까지 4보다 큰 값의 개수를 찾으면 됨